Электрическое сопротивление проводника
Электрическое сопротивление - физическая величина, которая показывает, какое препятствие создается току при его прохождении по проводнику. Единицами измерения служат Омы, в честь Георга Ома. В своем законе он вывел формулу для нахождения сопротивления, которая приведена ниже.
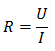
Рассмотрим сопротивление проводников на примере металлов. Металлы имеют внутреннее строение в виде кристаллической решетки. Эта решетка имеет строгую упорядоченность, а её узлами являются положительно заряженные ионы. Носителями заряда в металле выступают “свободные” электроны, которые не принадлежат определенному атому, а хаотично перемещаются между узлами решетки. Из квантовой физики известно, что движение электронов в металле это распространение электромагнитной волны в твердом теле. То есть электрон в проводнике движется со скоростью света (практически), и доказано, что он проявляет свойства не только как частица, но еще и как волна. А сопротивление металла возникает в результате рассеяния электромагнитных волн (то есть электронов) на тепловых колебаниях решетки и её дефектах. При столкновении электронов с узлами кристаллической решетки часть энергии передается узлам, вследствие чего выделяется энергия. Эту энергию можно вычислить при постоянном токе, благодаря закону Джоуля-Ленца – Q=I2Rt. Как видите чем больше сопротивление, тем больше энергии выделяется.
Удельное сопротивление
Существует такое важное понятие как удельное сопротивление, это тоже самое сопротивление, только в единице длины. У каждого металла оно свое, например у меди оно равно 0,0175 Ом*мм2/м, у алюминия 0,0271 Ом*мм2/м . Это значит, брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2 будет иметь сопротивление 0,0175 Ом, а такой же брусок, но из алюминия будет иметь сопротивление 0,0271 Ом. Выходит что электропроводность меди выше чем у алюминия. У каждого металла удельное сопротивление свое, а рассчитать сопротивление всего проводника можно по формуле
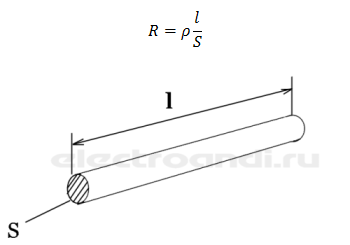
где p – удельное сопротивление металла, l – длина проводника, s – площадь поперечного сечения.
Значения удельных сопротивлений приведены в таблице удельных сопротивлений металлов (20°C)
|
Вещество |
p, Ом*мм2/2 |
α,10-3 1/K |
|
Алюминий |
0.0271 |
3.8 |
|
Вольфрам |
0.055 |
4.2 |
|
Железо |
0.098 |
6 |
|
Золото |
0.023 |
4 |
|
Латунь |
0.025-0.06 |
1 |
|
Манганин |
0.42-0.48 |
0,002-0,05 |
|
Медь |
0.0175 |
4.1 |
|
Никель |
0.1 |
2.7 |
|
Константан |
0.44-0.52 |
0.02 |
|
Нихром |
1.1 |
0.15 |
|
Серебро |
0.016 |
4 |
|
Цинк |
0.059 |
2.7 |
Кроме удельного сопротивления в таблице есть значения ТКС, об этом коэффициенте чуть позже.
Зависимость удельного сопротивления от деформаций
При холодной обработке металлов давлением, металл испытывает пластическую деформацию. При пластической деформации кристаллическая решетка искажается, количество дефектов становится больше. С увеличением дефектов кристаллической решетки, сопротивление течению электронов по проводнику растет, следовательно, удельное сопротивление металла увеличивается. К примеру, проволоку изготавливают методом протяжки, это значит, что металл испытывает пластическую деформацию, в результате чего, удельное сопротивление растет. На практике для уменьшения сопротивления применяют рекристаллизационный отжиг, это сложный технологический процесс, после которого кристаллическая решетка как бы, “расправляется” и количество дефектов уменьшается, следовательно, и сопротивление металла тоже.
При растяжении или сжатии, металл испытывает упругую деформацию. При упругой деформации вызванной растяжением, амплитуды тепловых колебаний узлов кристаллической решетки увеличиваются, следовательно, электроны испытывают большие затруднения, и в связи с этим, увеличивается удельное сопротивление. При упругой деформации вызванной сжатием, амплитуды тепловых колебаний узлов уменьшаются, следовательно, электронам проще двигаться, и удельное сопротивление уменьшается.
Влияние температуры на удельное сопротивление
Как мы уже выяснили выше, причиной сопротивления в металле являются узлы кристаллической решетки и их колебания. Так вот, при увеличении температуры, тепловые колебания узлов увеличиваются, а значит, удельное сопротивление также увеличивается. Существует такая величина как температурный коэффициент сопротивления (ТКС), который показывает насколько увеличивается, или уменьшается удельное сопротивление металла при нагреве или охлаждении. Например, температурный коэффициент меди при 20 градусах по цельсию равен 4.1 · 10 − 3 1/градус. Это означает что при нагреве, к примеру, медной проволоки на 1 градус цельсия, её удельное сопротивление увеличится на 4.1 · 10 − 3 Ом. Удельное сопротивление при изменении температуры можно вычислить по формуле
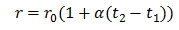
где r это удельное сопротивление после нагрева, r0 – удельное сопротивление до нагрева, a – температурный коэффициент сопротивления, t2 – температура до нагрева, t1 - температура после нагрева.
Подставив наши значения, мы получим: r=0,0175*(1+0.0041*(154-20))=0,0271 Ом*мм2/м. Как видите наш брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2, после нагрева до 154 градусов, имел бы сопротивление, как у такого же бруска, только из алюминия и при температуре равной 20 градусов цельсия.
Свойство изменения сопротивления при изменении температуры, используется в термометрах сопротивления. Эти приборы могут измерять температуру основываясь на показаниях сопротивления. У термометров сопротивления высокая точность измерений, но малые диапазоны температур.
На практике, свойства проводников препятствовать прохождению тока используются очень широко. Примером может служить лампа накаливания, где нить из вольфрама, нагревается за счет высокого сопротивления металла, большой длины и узкого сечения. Или любой нагревательный прибор, где спираль разогревается благодаря высокому сопротивлению. В электротехнике, элемент главным свойством которого является сопротивление, называется – резистор. Резистор применяется практически в любой электрической схеме.
