Последовательная RC-цепь
Рассмотрим последовательную RC-цепь, состоящую из последовательно соединенных резистора и конденсатора.
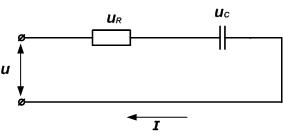
Напряжение на зажимах цепи
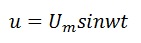
По второму закону Кирхгофа это же напряжение можно определить как сумму падений напряжений на резисторе и конденсаторе
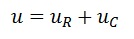
где
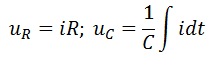
Тогда первое выражение можно переписать в следующем виде
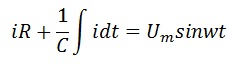
Ток в цепи равен
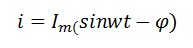
Подставив в выражение выше, и выполнив интегрирование, получим
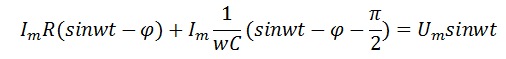
Напряжение на резисторе равно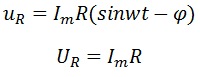
Напряжение на конденсаторе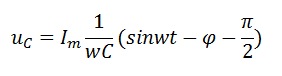
Как видно из последнего выражения напряжение на конденсаторе отстает от тока на угол π/2.
Реактивное (емкостное) сопротивление конденсатора равно
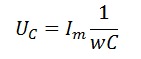
С уменьшением частоты емкостное сопротивление конденсатора увеличивается. При постоянном токе оно равно бесконечности, так как частота равна нулю.
Сдвиг фаз в последовательной RC – цепи можно определить по формуле
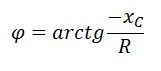
Полное сопротивление RC-цепи
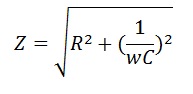
Амплитудное значение тока
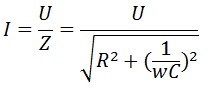
Рассмотрим пример решения задачи с RC-цепью
Полное сопротивление последовательной RC- цепи равно 24 Ом. Напряжение на резисторе равно 10 В, а его сопротивление 20 Ом. Найдите С, Uc, U, I, сдвиг фаз φ. Постройте векторную диаграмму.
Найдем ток, протекающий через резистор. Так как соединение последовательное, то этот ток будет общим для всей цепи.
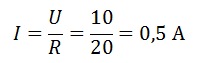
Зная ток и сопротивление цепи, найдем напряжение
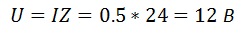
Емкостное сопротивление конденсатора
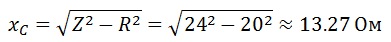
Зная сопротивление, найдем напряжение и емкость
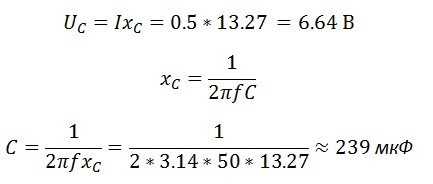
Сдвиг фаз
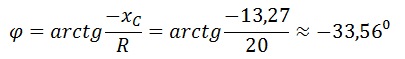
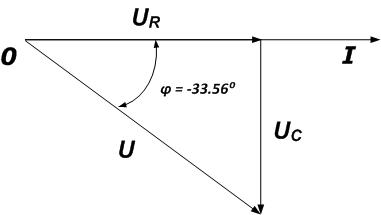
Построим векторную диаграмму RC – цепи, при этом учитываем, что напряжение на конденсаторе отстает от тока (это видно по знаку сдвига фаз).
Сначала откладывается вектор тока в цепи, затем напряжение на резисторе и напряжение на конденсаторе. Затем строится вектор общего напряжения как сумма векторов напряжений на конденсаторе и на резисторе.
Читайте также - Последовательная RL-цепь
